Atelier Bonryu(E)
pinhole photography
Laboratory: Pinhole Photography
History of Pinhole Photography
- Remark -
Remark#1: Aristotle’s Problem
Aristotle’s problem (Problemata Physica) is as follows.
Problem 6 (Book XV): Why is it the case that when the sun passes through quadri-laterals, as for instance in wickerwork, it does not produce a figure rectangular in shape but circular?
Problem 11 (Book XV): Why is it the case that an eclipse of the sun, if one looks at it through a sieve or through leaves, such as a plane-tree or other broadleaved tree, or if one joins the fingers of one hand over the fingers of the other, the rays are crescent-shaped where they reach the earth? Is it for the same reason as that when light shines through a rectangular peep-hole, it appears circular in the form of a cone?
In the west Aristotle’s problem remained unsolved until Francesco Maurolico (1494 - 1575) and Johannes Kepler (1571 - 1630) solved it in Renaissance. As Maurolico was living one generation before Kepler, obviously Maurolico solved the problem earlier than Kepler. However, Kepler published his result in his book ”Ad Vitellionem Paralipomera“ in 1604, but ”Photismi di Lumine et Umbra“ by Maurolico was published posthumously in 1611 which was 36 years after his death though Maurolico had written up the book already in 1521. Though both the solutions by Maurolico and Kepler are correct as shown later, their points of view are different. Kepler is said to have a knowledge apparently that these two solutions were equivalent and both the solutions satisfied his motivation to solve the Aristotle’s problem. In the following we explain both the solutions on the basis of “Theories of Vision” by David C. Lindberg by supplementing some equations and figures. There is an opinion that the result of Maurolico was already known in the community of scholars before publishing the above book and had affected the community.
Solution by Maurolico: Maurolico was born in Messina, Sicily. He entered the Benedictine Order and became a monk, and later an abbot at the Cattedorale San Nicolo di Messina. Outside the order he became head of the Messina mint, director of fortifications for the city, and in 1569 he was appointed professor of mathematics at the University of Messina. Throughout his lifetime he made large contributions to mathematics, optics, mechanics, and astronomy.
He considered image of a luminous source AB is produced by light passing through an aperture CD (Figure 1). AH, AG, BF, and BE are light rays radiated from the edges A and B of the luminous source which graze edges of the aperture, C and D. Triangles (cones in 3D) CEG and DFH are, respectively, formed by light rays from the vertexes C and D, bases of which are similar figures as the luminous source AB (see Figure 2 for the 3D case). As [the vertexes A and B are located further from the image plane than the vertexes C and D and] the angles ECG and FDH are larger than the angles EBF and GAH, lengths of the base lines EG and FH increase more rapidly than lengths of the base lines EF and GH with increasing the distance between the aperture and the image plane. This is more clearly expressed by using equations in the following, where the symbols in Figure 1 are used as, 
: size of the source, 
: size of the image of the source, 
: size of the aperture, 
: size of the image of the aperture, 
: distance between the source and the aperture, 
: distance between the aperture and the image plane. The sizes of the images of the luminous source and the aperture, and the ratio of them are derived as
As shown in these equations, the ratio of the image of the aperture to that of the luminous source decreases with increasing distance from the aperture to the image 
. Especially , in the case of a luminous source as the sun which is extremely large and located extremely far from the aperture (
), by defining angle of view ( 
) this equation is reduced to more intelligible form as
Because the ratio 
is nearly constant, the ratio of the size of the aperture image to the size of the source image decreases in inverse proportion to the distance between the aperture and the image plane 
, and the difference between two images EG and FH becomes negligible.
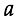
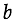
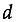
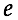
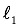
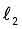
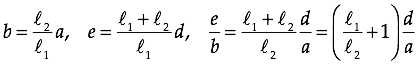
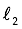
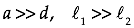
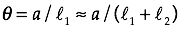
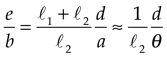
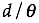
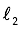
The same explanatory diagram for 3D case is given in Figure 2. The images of the luminous source ABCD are base rectangles (Ae-Be-Ce-De, Af-Bf-Cf-Df, Ag-Bg-Cg-Dg etc.) of piramids (e-Ae-Be-Ce-De, f-Af-Bf-Cf-Df, g-Ag-Bg-Cg-Dg, etc.)
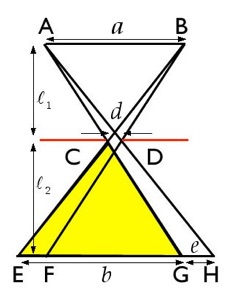
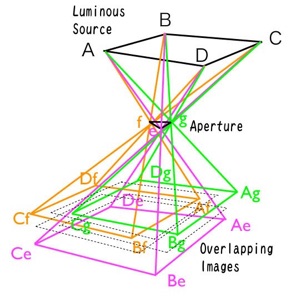
Figure 1
Solution by Maurolico (2D)
The ”final“ image is overlapped images (EG, FH, and so on) of the luminous source AB formed by lights intersecting within the aperture CD.
Figure 2
Solution by Maurolico (3D)
The ”final“ image is overlapped images (AeBeCeDe and so on) of the luminous source ABCD formed by lights intersecting within the aperture efg.
Solution by Kepler: When Kepler calculated the lunar diameter by observing the solar eclipse of July 10, 1600, he found that it was smaller than the diameter calculated from data obtained by Tycho Brahe by using a pinhole camera. During the course of investigating the reason of the disagreement he found a solution to the Aristotle’s problem. Differently from the Maurolico’s solution which was explained in 2D configuration, Kepler explained the phenomenon in 3D space as follows. In his case the luminous source was a rectangular book ABCD (Figure 4). He placed a book in high and between it and the floor he set a table having a many-cornered aperture (a triangle efg in the case of Figure 4). Then he sent down a thread from one corner of the book through the aperture onto the floor (e.g., a ray A-e-Ae). He moved the thread so that the point on the source was fixed and the thread grazed edges of the aperture(efg), and traced the intersecting point of the thread with the floor, which created a figure similar to the aperture (e.g., Ae-Af-Ag). If the same process is repeated for all the corners of the luminous source and for all of an indefinite number of points in the source inside the circumference, there resulted an indefinite number of traced figures of the aperture image on the ground, which produced a projected image of the luminous source, the book. Figure 3 shows the 2D explanation of this process.
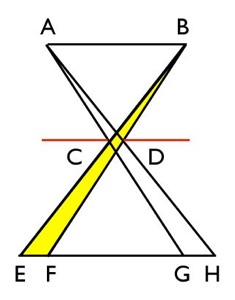
Figure 3
Solution of Kepler (2D)
The ”final“ image is overlapped images (EF, GH, and so on) of the aperture CD created by light rays from an indefinite number of points on the luminous source AB.
Figure 4
Solution of Kepler (3D)
The ”final“ image is overlapped triangular images (AeAgAf, BeBgBf, and so on) of the triangular aperture egf created by light rays from an indefinite number of points on the rectangular luminous source ABCD.
In summary, in order to create the ”final“ image, images of the luminous source were overlapped within the range of the shape of the aperture in the solution of Maurolico, and images of the aperture were overlapped within the range of the shape of the luminous source in the case of Kepler. Anyway though Kepler as well as Maurolico did not give quantitative evaluation on the blurring effect by the aperture, Maurolico described that the size of the image of the aperture became relatively small with increasing the distance to the image plane and Kepler described that overlapped images of the aperture became the image of the luminous source. The solutions by Maurolico and Kepler are essentially the same. By the way, Kepler got tips on the method to represent a light ray by a thread from the book, Four Books on Measurement (Underweysung der Messung mit dem Zirckel und Richtscheyt)(1525) by Albrecht Dürer.
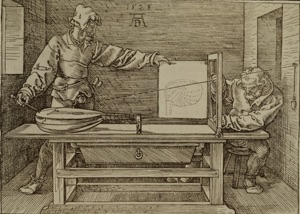
Man Drawing a Lute by Albrecht Dürer (1525)
A man is drawing a lute in perspective by using a thread.
